
Obwohl das Universum von Objekten mit wahrhaft gigantischen Ausmaßen bevölkert wird, nehmen wir die allermeisten davon nur als winzige Lichtpünktchen wahr. Mit Ausnahme des Bandes unserer Milchstraße, die quer über den Nachthimmel verläuft, erscheinen uns die anderen Objekte nicht sehr groß. Doch wie wird diese Größe gemessen? Und in welcher Einheit? Dieser Frage sind wir am 4. Kurstag nachgegangen.
Grad, Minuten, Sekunden und noch kleiner…
Das Maß, mit denen die perspektivische Größe von Gegenständen und anderen Objekten wahrgenommen werden kann, ist keine Länge, sondern ein Winkel. Je größer die winkelmäßige Ausdehnung eines Objektes ist, desto größer empfinden wir es; egal ob es sich dabei um einen Stern, ein Haus oder ein Regenschirm handelt. Die Sonne erscheint uns kleiner als ein Regenschirm, wenn wir diesen nur nahe genug an uns heranhalten.
Nach der Milchstraße sind Sonne und Mond die uns am zweitgrößten erscheinenden Objekte. Wenn man ihre Winkelausdehnung bestimmt hat, wird man sich wundern: Es sind jeweils nur knapp ein halbes Grad! Das kann ja heiter werden. Alle anderen Objekte erscheinen uns viel winziger, also mit 0.0000-Graden. Um auch mit ganz kleinen Winkelangaben jonglieren zu können, haben die Astronomen die Grad-Angaben (°) eines Winkels um Bruchteile – wie bei der Uhrzeit – erweitert: So ist 1/60 Grad eine (Bogen-)Minute mit einem Einzelobenstrich ‚ als Kennzeichnung und 1/60.tel Minute eine (Bogen-) Sekunde. Somit ist 1 Bogensekunde genau ein 1/3600.-tel Grad. Wahrlich winzig und doch handhabbar! Als Recheneinheit einer Bogensekunde wird üblicherweise arcsec (Arcus Sekans) oder der Doppelobenstrich “ verwendet.
Doch wie klein ist eigentlich die scheinbare Größe von einer Bogensekunde? Hierzu kann man sich eines Regenschirms bedienen. Wenn dieser einen Durchmesser von 1,50 m besitzt, sehen wird diesen unter einem Winkel von einer Bogensekunde, wenn dieser von uns mehr als 300 km entfernt ist! Das ist wirklich winzig, doch den Astronomen noch nicht winzig genug. Die visuelle Größenausdehnung von Planeten oder die Eigenbeweung von Sternen sind noch viel, viel kleiner wahrzunehmen. Herzu bedient man sich der Millibogensekunde, also 1/1000 Bogensekunde (Einheit masx) oder auch der Mikrobogensekunde (entspricht einem Millionstel einer Bogensekunde – Einheit µas).
Etwas abgehobene Mathematik: Die Trigonometrie
Wie man schon ahnt, hängt die Winkelausdehnung, unter dem wir einen Gegenstand sehen, nicht nur allein von der Größe, sondern auch von seiner Entfernung ab: Je weiter entfernt wir uns befinden, desto kleiner erscheint uns ein Objekt (Scheinriesen einmal ausgenommen). Die folgende Grafik soll das etwas genauer beleuchten:
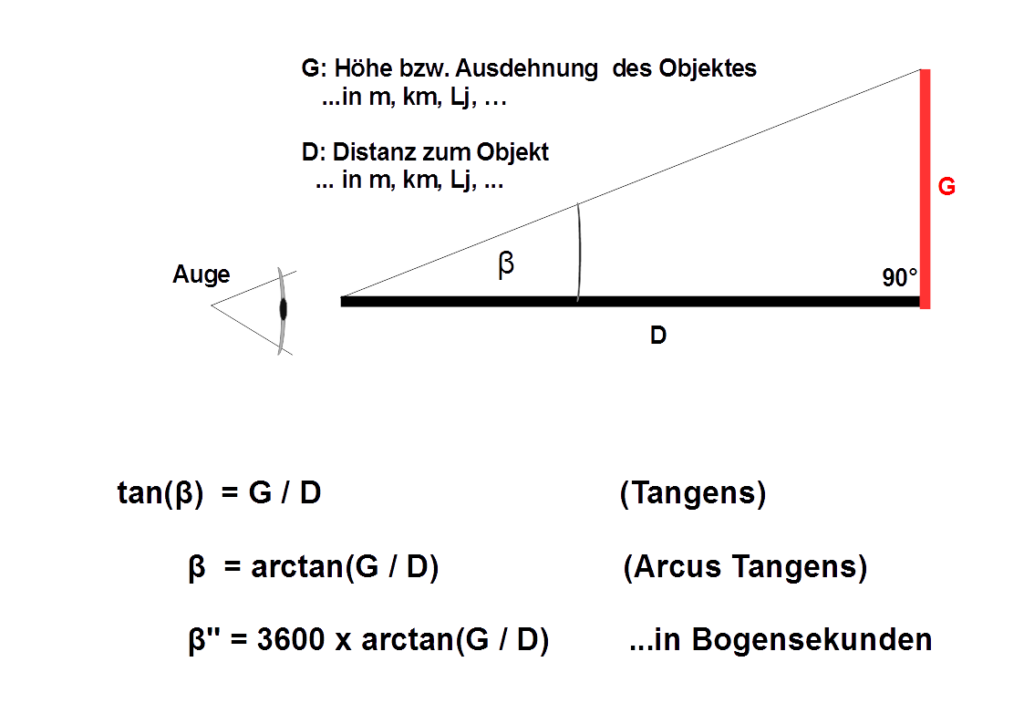
Der Quotient aus Objektgröße und Entfernung ist eine sog. trigometrische Größe (der Tangens ‚tan‘) des eingeschlossenen Winkels. Um den Winkel mit dem Taschenrechner berechnen zu können, muss man zunächst den Quotienten aus Objektgröße und Entfernung (bei beiden muss zwingend die gleiche Längeneinheit verwendet werden) bestimmen.
Um den Winkelwert in Grad zu berechnen, muss der Taschenrechner im DEG-Modus laufen (man erkennt es normalerweise im DEG-Zeichen im Display). Danach tippt man auf dem Taschenrechner die Taste [ATAN] oder [TAN-1]. Der Taschenrechner gibt nun den Zahlenwert des Winkels in Grad zurück.
Bei sehr weit entfernten Objekten können wir natürlich sehr kleine Gradangaben bekommen. Multiplizieren (‚Plutimizieren‘ wie Pippi Langstrumpf sagt) wir dieses Ergebnis jedoch mit 3600, so erhalten wir die Bogensekunden. Das ist schon viel handlicher!
Die Top Ten
Sehen wir einmal von der Milchstraße ab, können wir die Liste der Top-10 der uns mit bloßem Auge am größten erscheinenden Objekte am Himmel aufstellen – mit überraschendem 3. Platz:
- Platz – Unsere Sonne. Maximale Winkelausdehnung: 31’54“
- Platz – Der Mond. Maximale Winkelausdehnung: 31’06“
- Platz – Visuell wahrnehmbarer Kernbereich des Andromedanebels: ca. 65“
- Platz – Venus. Maximale Winkelausdehung: 60“
- Platz – Jupiter: Maximale Winkelausdehung: 45“
- Platz – Mars: Maximale Winkelausdehung: 25“
- Platz – Merkur: Maximale Winkelausdehung: 13 “
- Platz – Saturn: Maximale Winkelausdehung: 11“
- Platz – Uranus: Maximale Winkelausdehung: 4“
- Platz – Neptun: Maximale Winkelausdehung: 2“
Weitere wissenswerte Winkelgrößen betreffen:
- Auflösungsvermögen des menschlichen Auges: 60“
- Auflösungsvermögen der Erdatmosphäre: 1“ – 5“ (Seeing, in unseren mitteleuropäischen Breiten ca. 3“)


2 Kommentare
Detlef · 2. Oktober 2020 um 12:16
Hallo Frank, vielen Dank für Deine Nachbereitung des letzten Themas zur Entfernungsbestimmung im Kosmos.
Mir ist folgendes aufgefallen:
„Wie man schon ahnt, hängt die Winkelausdehnung, unter dem wir einen Gegenstand sehen, von seiner Entfernung und von der Distanz ab:“
Gemeint ist bestimmt: Wie man schon ahnt, hängt die Winkelausdehnung, unter dem wir einen Gegenstand sehen, von seiner Entfernung und von der Objektgröße ab.
🙂
VG
Detlef T.
Albire0 · 2. Oktober 2020 um 20:59
Ja, das war ein Versehen. Ist bereits korrigiert!
Die Kommentare sind geschlossen.