Am siebenten Kurstag gingen wir der Frage nach, wie man die Entfernung von Sternen bestimmen kann. Die Antwort hat etwas mit der Erde zu tun…
Man kennt des Rätsels Lösung bereits als banalen Alltagseffekt: Streckt man den Zeigefinger aus und hält ihn in kurzer Distanz vor das Gesicht und hält sich abwechselnd das linke und dann das rechte Auge zu, so sieht man, dass der Hintergrund hinter dem Zeigefinger mal rechts und mal links verschoben ist. Diesen Perspektiveneffekt nennt man Parallaxe.
Ein Gedankenexperiment
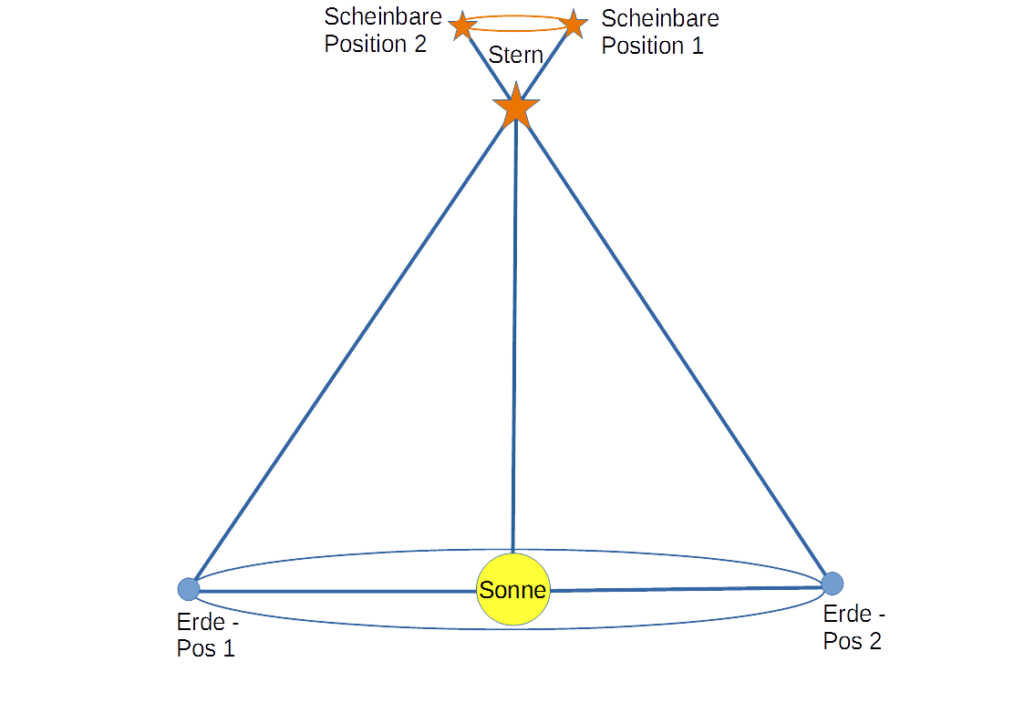
Die Parallaxe ist uns am vorletzten Kurstag schon einmal über den Weg gelaufen, als es um die Definition des Parsecs (3.26 Lichtjahre) ging: Ein Stern befindet sich genau dann in einer Entfernung von einem Parsec von der Sonne, wenn der Abstand Erde – Sonne (also eine Astronomische Einheit) vom Stern aus betrachtet gerade einem Öffnungswinkel von einer Bogensekunde (1/3600-tel Grad) entspricht. Genau genommen wird vorausgesetzt, dass sich der Stern senkrecht zur Ekliptik befindet.
Dreht man das ganze nun um und fragt sich, wie dieselbe Situation von der Erde aus betrachtet aussehen würde, so erkennt man, dass der ein Parsec entfernte Stern sich innerhalb eines halben Jahres um zwei Bogensekunden vor dem fernen Sternenhintergrund bewegt hat: Ja, zwei Bogensekunden – nach einer halben Sonnenumrundung ist die Erde nun auf der gegenüberliegenden Seite angekommen; dies entspricht dem Durchmesser (und nicht dem Radius) der Erdbahn um die Sonne – also zwei Astronomische Einheiten. Ein weiteres halbes Jahr später ist der Stern dann wieder auf seine Ursprungsposition zurückgekehrt (mal von seiner Eigenbewegung abgesehen).
Winzige Kreisbähnchen
Ein Stern, der ein Parsec von der Erde entfernt wäre, beschriebe im Laufe eines Jahres eine winzige scheinbare Kreisbahn von einem Öffnungswinkel von zwei Bogensekunden vor dem fernen Sternhintergrund. Der Abstand vom Mittelpunkt dieser kleinen scheinbaren Kreisbahn, der Parallaxenwinkel, beträgt dabei genau eine Bogensekunde senkrecht zur Ekliptik.
Allerdings sind alle bislang gefundenen Parallaxenwinkel von Sternen sehr viel kleiner als eine Bogensekunde – kein Wunder; denn der nächst gelegene Stern ist ja auch 4.3 Lichtjahre, also 1.32 Parsec entfernt.
Je größer die Entfernung Sonne -Stern ist, desto langgezogener wird das Dreick Stern – Sonne – Erde und umso kleiner wird der Öffnungswinkel. Doch wir groß ist eigentlich so ein Parallaxenwinkel in Wirklichkeit?
Eine Beispielrechnung
Nehmen wir an, ein Stern sei 50 Lichtjahre entfernt und er steht quasi senkrecht über der Ekliptik. Dann entspricht die Entfernung
50 / 3.26 Pc = 15.34 Pc. Wenn 1 Pc nun einer Bogensekunde entpricht, so sind dies bei 15.34 Pc also 1/15.34 Bogensekunden = 0.065 Bogensekunden oder 65 mas (Millibogensekunden). Der Stern beschreibt also eine scheinbare Kreisbahn vor dem fernen Himmelshintergrund mit einem Gesamtöffnungswinkel von von 2*65 mas = 130 Millibogensekunden.
Dieses Verfahren zur Bestimmung der Sternentfernungen hat natürlich seine Grenzen. Sehr weit entfernte Sterne beschreiben unfassbar kleine Parallaxenwinkel, diese sind dann kaum mehr messbar. Doch es gibt noch andere Methoden…