Die Vorspeise
Goldener Henkel, kurz nach dem zunehmenden Halbmond
An diesem VHS-Mittwoch gab es ein volles astronomisches Drei-Gänge-Menü. Zur ‚Vorspeise‘ haben wir ein Phänomen besprochen, welches kurz nach dem zunehmenden Halbmond auftritt: Die Sichtbarkeit des Goldenen Henkels. An der Schattengrenze des Mondes, an der besonders plastisch die vielen Krater, Gräben und Hänge der Mondoberfläche zu Tage treten, gibt es im Nordbereich am Sinus Iridium das Jura-Ringgebirge, dessen Höhen bereits von der Sonne beschienen werden, während die vorgelagerte Ebene noch im Dunklen verharrt. Diesen Bogen, der sich in den noch unbeleuchteten Teil des Mondes hineinstreckt, nennt man den ‚Goldenen Henkel‘. Am Sonntag, den 2. November, konnte man dieses Phänomen gut beobachten; es war ausnahmsweise mal für kurze Zeit sternenklar.
Das Hauptmenü
Drehbare Sternkarte – November 2014
Als Hauptgang haben wir uns die klassische drehbare Sternkarte vorgenommen. Wir konnten mit ihr sehen, was wir wegen dem bedeckten Himmel leider immer noch nicht konnten: Die momentane Position der Sternbilder über unseren Köpfen. Anhand das äußeren Sternkarten-Kreises, auf welchem die Monate und Tage des Jahres als Skalierung angebracht sind und des inneren, drehbaren Kreises, der eine 24-Stunden -Skalierung aufweist, konnten wir unterschiedliche Fragen beantworten; etwa: Wann geht der Orion am 5. November auf? Welches Tierkreis-Sternbild ist am Morgen des 6. Novembers zu sehen? Oder: Welche Sternbilder sind zirkumpolar; gehen also in unseren Breiten niemals unter?
Dessert
Frühlinspunkt im Zenit
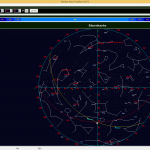
Doch der ‚Nachtisch‘ erwies sich mal wieder als schwer verdaulich. Selbst ich als Kurzleiter kam so richtig ins Schwitzen, als es darum ging, die Sternzeit, die Rektazension und den Stundenwinkel zu erklären; ohne Begriffe von ‚Koordinatentransformation‘ oder ‚Rotierende und nicht rotierende Bezugssysteme‘ verwenden zu müssen. Als Hilfestellung diente uns die elektronische Sternkarte der Astronomie-Software ‚Albireo‘, denn hier konnten wir uns den Schnittpunkt der aufsteigenden Ekliptik mit dem Himmelsäquator (den Frühlingspunkt) ansehen; und zwar in ‚Echtzeit‘. Denn dieser sog. ‚Widderpunkt‘ dient bei der Sternzeit und der Rektazension als Bezugsnullpunkt.
Auch die Sternzeit, die ja die wirkliche Eigenrotation der Erde gegenüber dem fernen Fixsternhimmel beschreibt, bezieht sich mit ihrem Mitternachtspunkt auf diesen abstrakten Punkt im Raum. Ein Sternenzeittag ist 23h und 56 Minuten lang; es fehlen also 4 Minuten zum Sonnenzeittag, da die Erde während der 24 Stunden auf ihrem Weg um die Sonne weitergezogen ist.
Die Sternzeit zeigt also 0:00 Uhr an, wenn dieser Widerpunkt, der im Sternbild der Fische liegt, gerade am höchsten im Süden steht; also ‚kulminiert‘. Danach geht es dann analog zur ’normalen‘ Uhrzeit weiter, bis dieser Widderpunkt nach 23h und 56 Minuten wieder dort angekommen ist. So gesehen bedeutet die Sternzeit nicht nur eine weitere Zeit-Definition, sondern sie beschreibt mit jedem Sternzeitpunkt eine feste Richtung im Raum.
Der Stundenwinkel ist der Winkel an einer parallaktischen Montierung, der an der Stundenachse eingestellt werden muss, damit das Teleskop (zusammen mit der Deklination) auf einen bestimmten Stern am Himmel gerichtet werden kann.
Rektazension (und Deklination) beschreiben die festen Koordinaten auf der ‚Himmelsspähre‘, mit denen die Sterne und andere Objekte des extraplanetaren Raumes in den Sternkatalogen verzeichnet sind. Sie entsprechen der geografischen Länge und der geografischen Breite auf der Erde.
Für Stundenwinkel H, Sternzeit SZ und Rektazension RA besteht folgende Beziehung:
H = S – RA
Für den Stundenwinkel H=0 ergibt sich daraus S=RA. Das bedeutet: Wenn ein Stern kulminiert – also exakt im Süden (Stundenwinkel H ist 0:00) steht – entspricht die momentane Sternzeit der Raktazensionskoordinate des Sterns (ebenso exakt).
Weiterhin gilt für die Sternzeit, dass sie eine lokale Zeit ist. Das bedeutet, dass Beobachter, die sich auf unterschiedlichen Längengraden befinden, einen Stern zu unterschiedlichen Sternenzeiten wahrnehmen. Man kann die Sternzeit nach folgender Formel berechnen:
Sternzeit = (Geografische Länge + Monatstag)*4 + doppelte Monatszahl + MEZ + 3h:26Minuten
(nach: Hans Oberndorfer, Schau mal in die Sterne, Kosmos Naturführer)